3 Awesome Visualization Techniques for every dataset

Visualizations are awesome. However, a good visualization is annoyingly hard to make.
Moreover, it takes time and effort when it comes to present these visualizations to a bigger audience.
We all know how to make Bar-Plots, Scatter Plots, and Histograms , yet we don’t pay much attention to beautify them.
This hurts us - our credibility with peers and managers. You won’t feel it now, but it happens.
Also, I find it essential to reuse my code. Every time I visit a new dataset do I need to start again? Some reusable ideas of graphs that can help us to find information about the data FAST.
In this post, I am also going to talk about 3 cool visual tools:
- Categorical Correlation with Graphs,
- Pairplots,
- Swarmplots and Graph Annotations using Seaborn.
In short, this post is about useful and presentable graphs.
I will be using data from FIFA 19 complete player dataset on kaggle - Detailed attributes for every player registered in the latest edition of FIFA 19 database.
Since the Dataset has many columns, we will only focus on a subset of categorical and continuous columns.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# We dont Probably need the Gridlines. Do we? If yes comment this line
sns.set(style="ticks")
player_df = pd.read_csv("../input/data.csv")
numcols = [
'Overall',
'Potential',
'Crossing','Finishing', 'ShortPassing', 'Dribbling','LongPassing', 'BallControl', 'Acceleration',
'SprintSpeed', 'Agility', 'Stamina',
'Value','Wage']
catcols = ['Name','Club','Nationality','Preferred Foot','Position','Body Type']
# Subset the columns
player_df = player_df[numcols+ catcols]
# Few rows of data
player_df.head(5)

This is a nicely formatted data, yet we need to do some preprocessing to the Wage and Value columns(as they are in Euro and contain strings) to make them numeric for our subsequent analysis.
def wage_split(x):
try:
return int(x.split("K")[0][1:])
except:
return 0
player_df['Wage'] = player_df['Wage'].apply(lambda x : wage_split(x))
def value_split(x):
try:
if 'M' in x:
return float(x.split("M")[0][1:])
elif 'K' in x:
return float(x.split("K")[0][1:])/1000
except:
return 0
player_df['Value'] = player_df['Value'].apply(lambda x : value_split(x))
Categorical Correlation with Graphs:
In Simple terms, Correlation is a measure of how two variables move together.
For example, In the real world, Income and Spend are positively correlated. If one increases the other also increases.
Academic Performance and Video Games Usage is negatively correlated. Increase in one predicts a decrease in another.
So if our predictor variable is positively or negatively correlated with our target variable, it is valuable.
I feel that Correlations among different variables are a pretty good thing to do when we try to understand our data.
We can create a pretty good correlation plot using Seaborn easily.
corr = player_df.corr()
g = sns.heatmap(corr, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, annot=True, fmt='.2f', cmap='coolwarm')
sns.despine()
g.figure.set_size_inches(14,10)
plt.show()
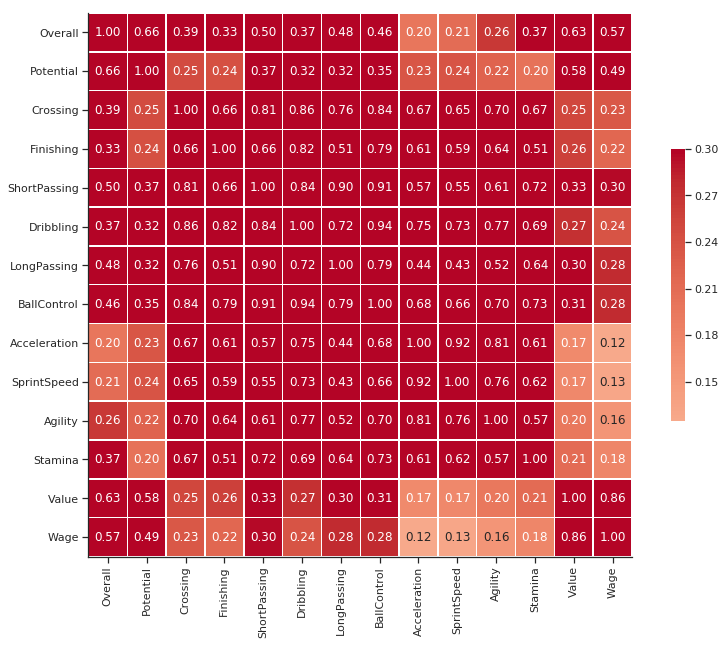
But do you notice any problem?
Yes, this graph only calculates Correlation between Numerical columns.
What if my target variable is Club or Position?
I want to be able to get a correlation among three different cases, and we use the following metrics of correlation to calculate these:
1. Numerical Variables
We already have this in the form of Pearson’s Correlation which is a measure of how two variables move together. This Ranges from [-1,1]
2. Categorical Variables
We will use Cramer’s V for categorical-categorical cases. It is the intercorrelation of two discrete variables and used with variables having two or more levels. It is a symmetrical measure as in the order of variable does not matter. Cramer(A,B) == Cramer(B,A).
For Example: In our dataset, Club and Nationality must be somehow correlated.
Let us check this using a stacked graph which is an excellent way to understand distribution between categorical vs. categorical variables. Note that we use a subset of data since there are a lot of nationalities and club in this data.
We keep only the best teams(Kept FC Porto just for more diversity in the sample)and the most common nationalities.
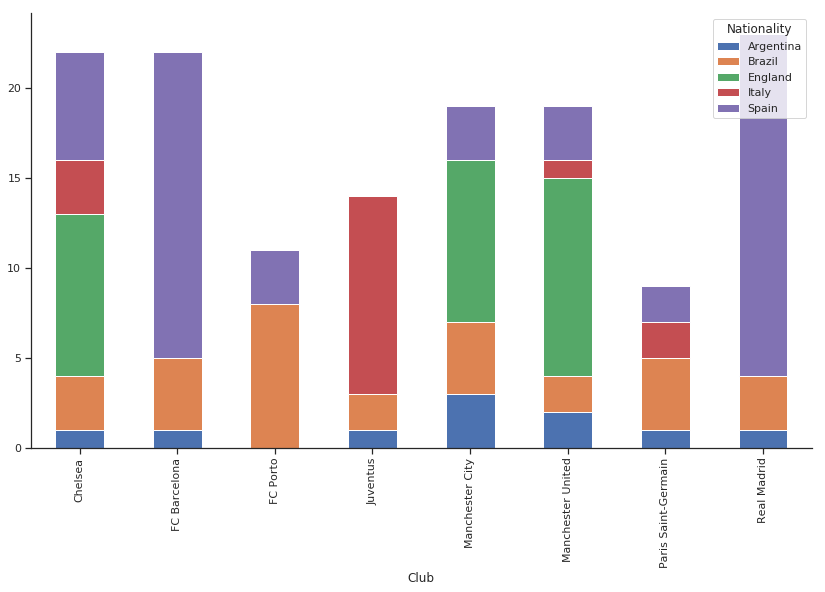
Note that Club preference says quite a bit about Nationality: knowing the former helps a lot in predicting the latter.
We can see that if a player belongs to England, it is more probable that he plays in Chelsea or Manchester United and not in FC Barcelona or Bayern Munchen or Porto.
So there is some information present here. Cramer’s V captures the same information.
If all clubs have the same proportion of players from every nationality, Cramer’s V is 0.
If Every club prefers a single nationality Cramer’s V ==1, for example, all England player play in Manchester United, All Germans in Bayern Munchen and so on.
In all other cases, it ranges from [0,1]
3. Numerical and Categorical variables
We will use the Correlation Ratio for categorical-continuous cases.
Without getting into too much Maths, it is a measure of Dispersion.
Given a number can we find out which category it belongs to?
For Example:
Suppose we have two columns from our dataset: SprintSpeed and Position:
- GK: 58(De Gea),52(T. Courtois), 58(M. Neuer), 43(G. Buffon)
- CB: 68(D. Godin), 59(V. Kompany), 73(S. Umtiti), 75(M. Benatia)
- ST: 91(C.Ronaldo), 94(G. Bale), 80(S.Aguero), 76(R. Lewandowski)
As you can see these numbers are pretty predictive of the bucket they fall into and thus high Correlation Ratio.
If I know the sprint speed is more than 85, I can definitely say this player plays at ST.
This ratio also ranges from [0,1]
The code to do this is taken from the dython package. I won’t write too much into code which you can anyway find in my Kaggle Kernel . The final result looks something like:
player_df = player_df.fillna(0)
results = associations(player_df,nominal_columns=catcols,return_results=True)
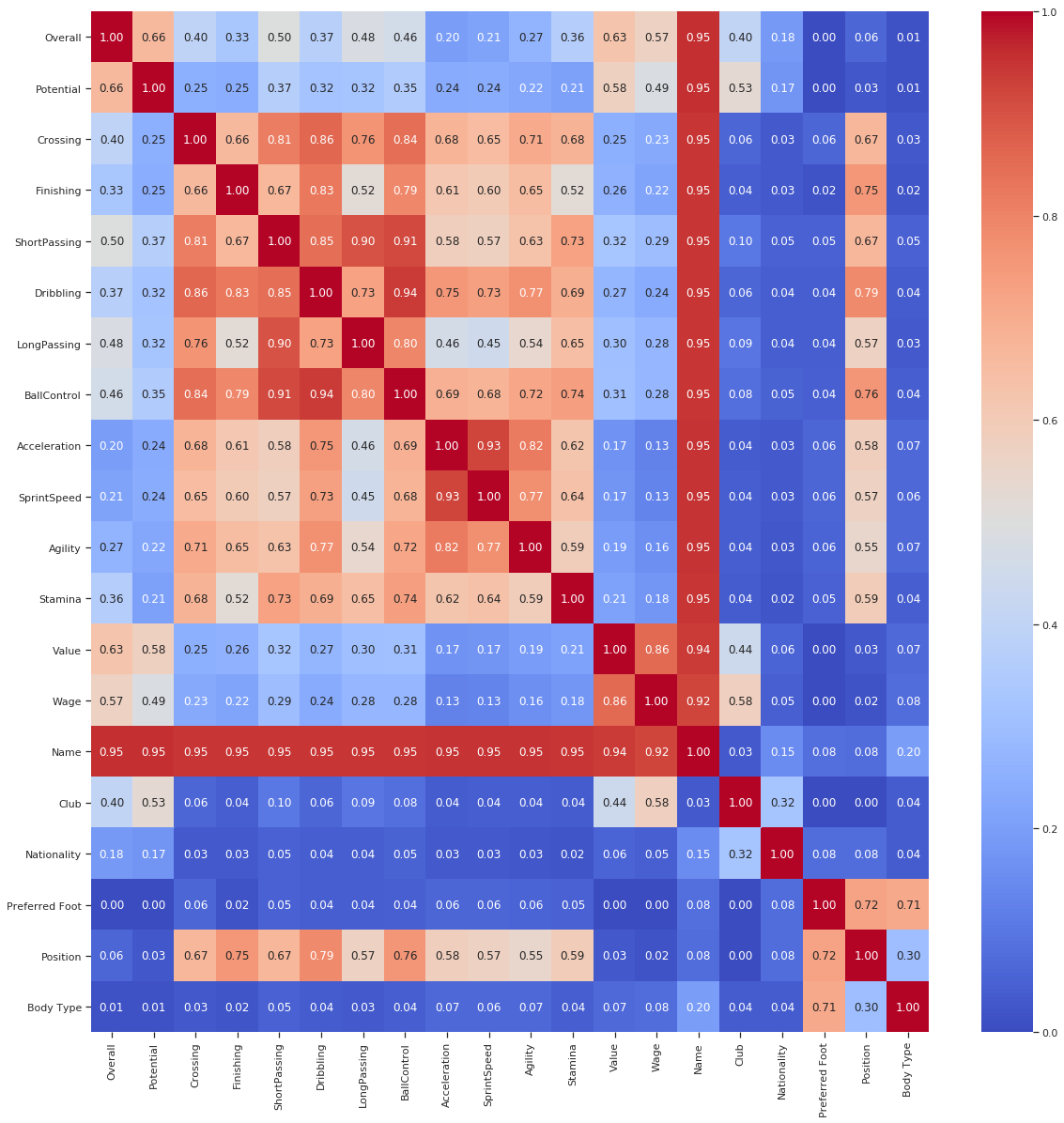
Isn’t it Beautiful?
We can understand so much about Football just by looking at this data. For Example:
The position of a player is highly correlated with dribbling ability. You won’t play Messi at the back. Right?
Value is more highly correlated with passing and ball control than dribbling. The rule is to pass the ball always. Neymar I am looking at you.
Club and Wage have high Correlation. To be expected.
Body Type and Preferred Foot is correlated highly. Does that mean if you are Lean, you are most likely left-footed? Doesn’t make much sense. One can investigate further.
Moreover, so much info we could find with this simple graph which was not visible in the typical correlation plot without Categorical Variables.
I leave it here at that. One can look more into the chart and find more meaningful results, but the point is that this makes life so much easier to find patterns.
Pairplots
While I talked a lot about correlation, it is a fickle metric.
To understand what I mean let us see one example.
Anscombe’s quartet comprises four datasets that have nearly identical Correlation of 1, yet have very different distributions and appear very different when graphed.
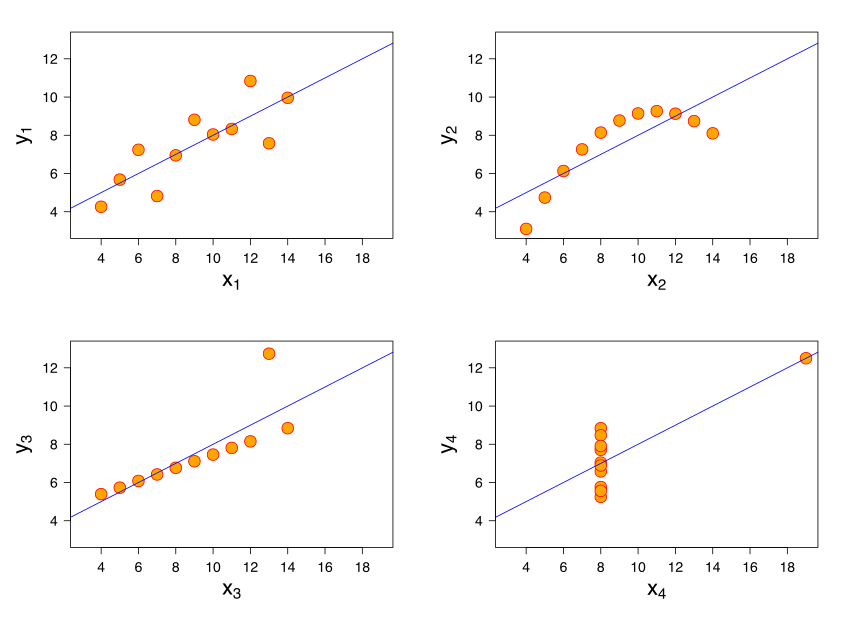
Thus sometimes it becomes crucial to plot correlated data. And see the distributions individually.
Now we have many columns in our dataset. Graphing them all would be so much effort.
No, it is a single line of code.
filtered_player_df = player_df[(player_df['Club'].isin(['FC Barcelona', 'Paris Saint-Germain',
'Manchester United', 'Manchester City', 'Chelsea', 'Real Madrid','FC Porto','FC Bayern München'])) &
(player_df['Nationality'].isin(['England', 'Brazil', 'Argentina',
'Brazil', 'Italy','Spain','Germany']))
]
# Single line to create pairplot
g = sns.pairplot(filtered_player_df[['Value','SprintSpeed','Potential','Wage']])
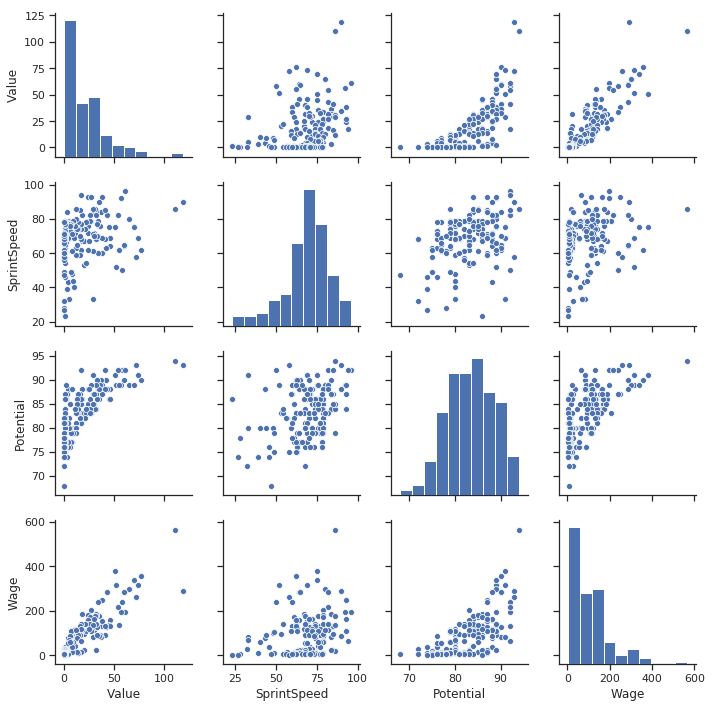
Pretty Good. We can see so much in this graph.
Wage and Value are highly correlated.
Most of the other values are correlated too. However, the trend of potential vs. value is unusual. We can see how the value increases exponentially as we reach a particular potential threshold. This information can be helpful in modeling. Can use some transformation on Potential to make it more correlated?
Caveat: No categorical columns.
Can we do better? We always can.
g = sns.pairplot(filtered_player_df[['Value','SprintSpeed','Potential','Wage','Club']],hue = 'Club')
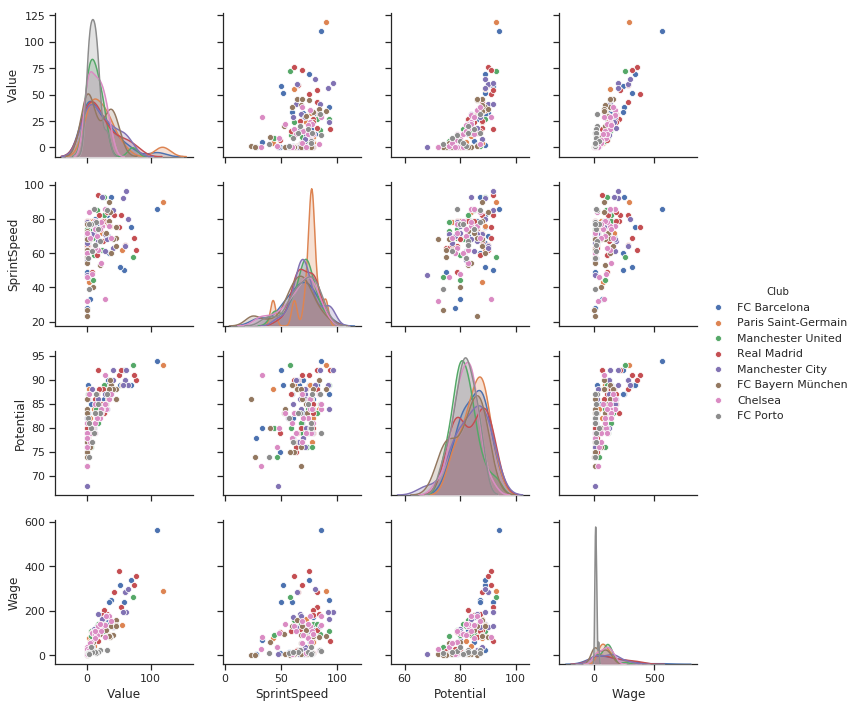
So much more info. Just by adding the hue parameter as a categorical variable Club.
- Porto’s Wage distribution is too much towards the lower side.
- I don’t see that steep distribution in value of Porto players. Porto’s players would always be looking out for an opportunity.
- See how a lot of pink points(Chelsea) form sort of a cluster on Potential vs. wage graph. Chelsea has a lot of high potential players with lower wages. Needs more attention.
I already know some of the points on the Wage/Value Subplot.
The blue point for wage 500k is Messi. Also, the orange point having more value than Messi is Neymar.
Although this hack still doesn’t solve the Categorical problem, I have something cool to look into categorical variables distribution. Though individually.
SwarmPlots
How to see the relationship between categorical and numerical data?
Enter into picture Swarmplots, just like their name. A swarm of points plotted for each category with a little dispersion on the y-axis to make them easier to see.
They are my current favorite for plotting such relationships.
g = sns.swarmplot(y = "Club",
x = 'Wage',
data = filtered_player_df,
# Decrease the size of the points to avoid crowding
size = 7)
# remove the top and right line in graph
sns.despine()
g.figure.set_size_inches(14,10)
plt.show()
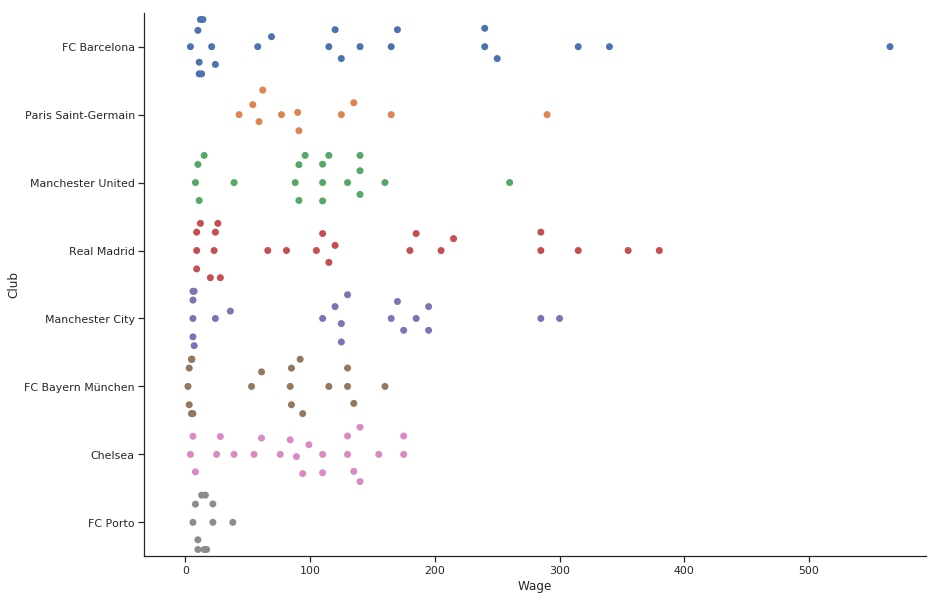
Why don’t I use Boxplots? Where are the median values? Can I plot that? Obviously. Overlay a bar plot on top, and we have a great looking graph.
g = sns.boxplot(y = "Club",
x = 'Wage',
data = filtered_player_df, whis=np.inf)
g = sns.swarmplot(y = "Club",
x = 'Wage',
data = filtered_player_df,
# Decrease the size of the points to avoid crowding
size = 7,color = 'black')
# remove the top and right line in graph
sns.despine()
g.figure.set_size_inches(12,8)
plt.show()
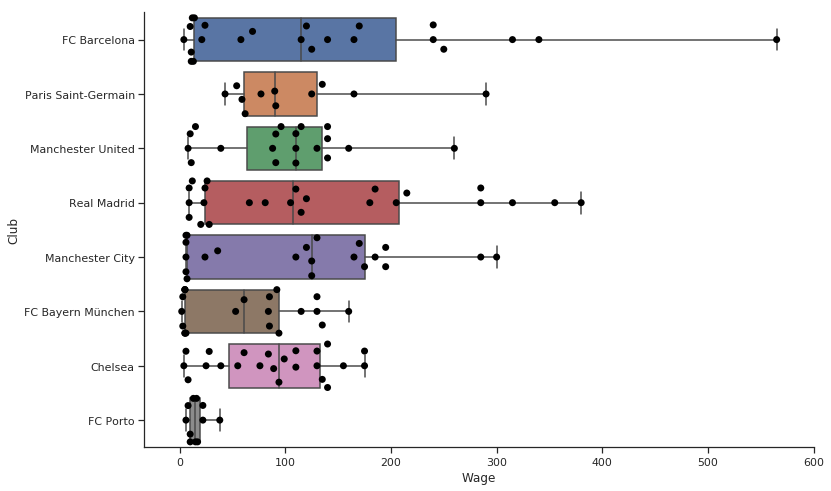
Pretty good. We can see the individual points on the graph, see some statistics and understand the wage difference categorically.
The far right point is Messi. However, I should not have to tell you that in a text below the chart. Right?
This graph is going to go in a presentation. Your boss says. I want to write Messi on this graph. Comes into picture annotations.
max_wage = filtered_player_df.Wage.max()
max_wage_player = filtered_player_df[(player_df['Wage'] == max_wage)]['Name'].values[0]
g = sns.boxplot(y = "Club",
x = 'Wage',
data = filtered_player_df, whis=np.inf)
g = sns.swarmplot(y = "Club",
x = 'Wage',
data = filtered_player_df,
# Decrease the size of the points to avoid crowding
size = 7,color='black')
# remove the top and right line in graph
sns.despine()
# Annotate. xy for coordinate. max_wage is x and 0 is y. In this plot y ranges from 0 to 7 for each level
# xytext for coordinates of where I want to put my text
plt.annotate(s = max_wage_player,
xy = (max_wage,0),
xytext = (500,1),
# Shrink the arrow to avoid occlusion
arrowprops = {'facecolor':'gray', 'width': 3, 'shrink': 0.03},
backgroundcolor = 'white')
g.figure.set_size_inches(12,8)
plt.show()
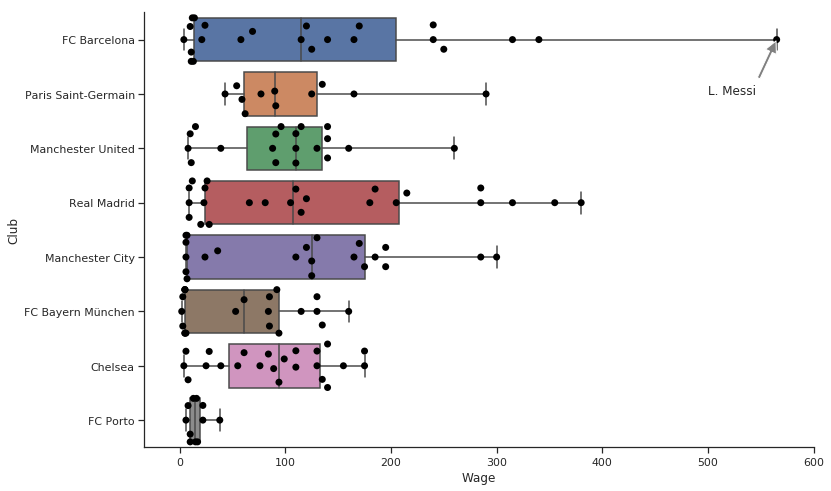
- See Porto Down there. Competing with the giants with such a small wage budget.
- So many Highly paid players in Real and Barcelona.
- Manchester City has the highest median Wage.
- Manchester United and Chelsea believes in equality. Many players clustered in around the same wage scale.
- I am happy that while Neymar is more valued than Messi, Messi and Neymar have a huge Wage difference.
A semblance of normalcy in this crazy world.
So to recap, in this post, we talked about calculating and reading correlations between different variable types, plotting correlations between numerical data and Plotting categorical data with Numerical data using Swarmplots. I love how we can overlay chart elements on top of each other in Seaborn.
Also if you want to learn more about Visualizations, I would like to call out an excellent course about Data Visualization and applied plotting from the University of Michigan which is a part of a pretty good Data Science Specialization with Python in itself. Do check it out
If you liked this post, do look at my other post on Seaborn too where I have created some more straightforward reusable graphs. I am going to be writing more beginner friendly posts in the future too. Follow me up at Medium or Subscribe to my blog to be informed about them. As always, I welcome feedback and constructive criticism and can be reached on Twitter @mlwhiz
Code for this post in this kaggle kernel .
