Solve almost every Binary Search Problem

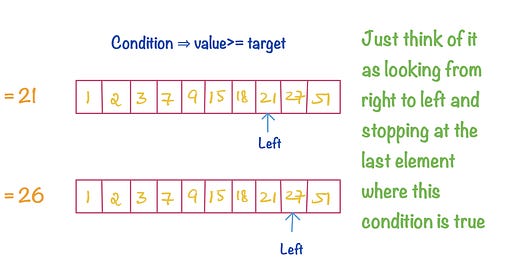
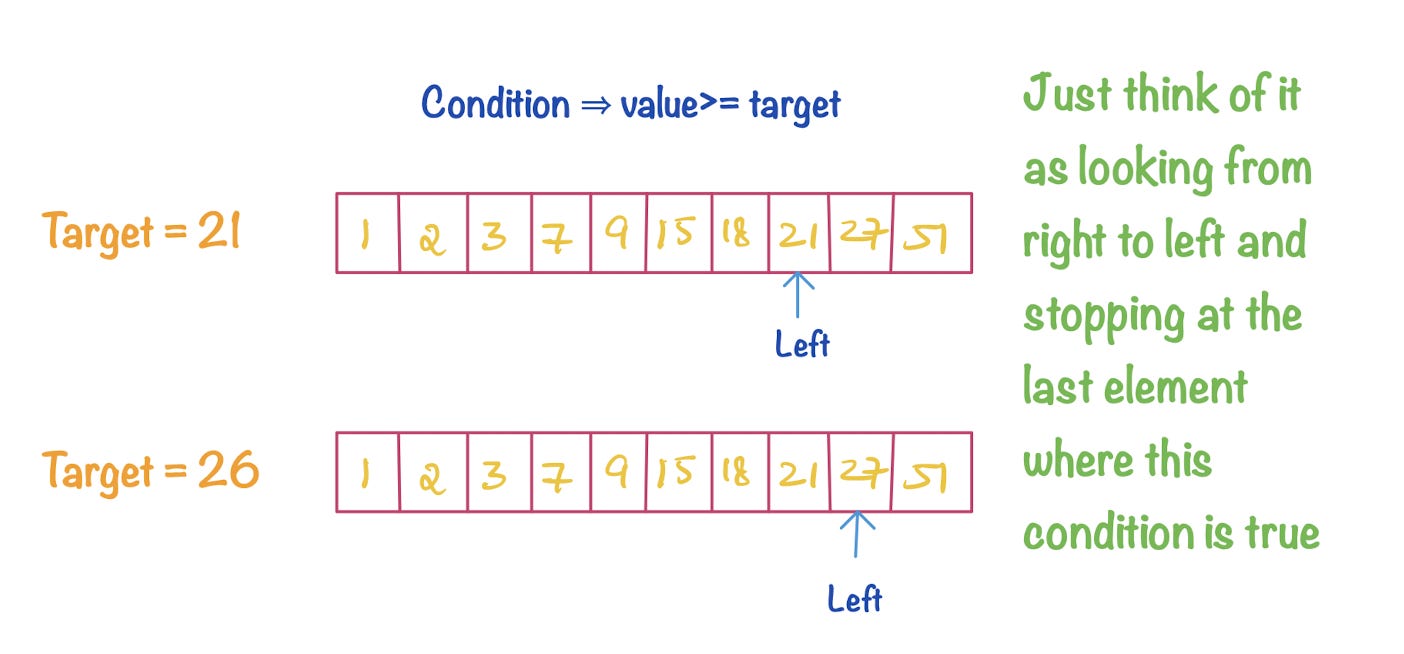
Algorithms are an integral part of data science. While most of us data scientists don’t take a proper algorithms course while studying, they are important all the same. Many companies ask data structures and algorithms as part of their interview process for hiring data scientists.

Now the question that many people ask here is what is the use of asking a data scientist such questions. The way I like to describe it is that a data structure question may be thought of as a coding aptitude test.

We all have given aptitude tests at various stages of our life, and while they are not a perfect proxy to judge someone, almost nothing ever really is. So, why not a standard algorithm test to judge people’s coding ability. But let’s not kid ourselves, they will require the same zeal to crack as your Data Science interviews, and thus, you might want to give some time for the study of algorithms.

This series of posts is about fast-tracking that study and panning some essential algorithms concepts for the data scientists in an easy to understand way.

In this post, I would particularly talk about Binary search.

What is Binary Search?

Let us say we have a sorted array of numbers, and we want to find out a number from this array. We can go the linear route that checks every number one by one and stops if it finds the number. The problem is that it takes too long if the array contains millions of elements. Here we can use a Binary search.

This is case of a recursion based algorithm where we make use of the fact that the array is sorted. Here we recursively look at the middle element and see if we want to search in the left or right of the middle element. This makes our searching space go down by a factor of 2 every step. And thus the run time of this algorithm is O(logn) as opposed to O(n) for linear search.

Another Way of Looking at Binary Search

While understanding how Binary search works is easy, there are a lot of problems when you go on to implement binary search. I myself am never able to implement Binary Search without a single mistake and do some mistake on equality signs or the search space. But this post by zhijun_liao was a godsend when it comes to understanding Binary search.

Essentially what this post suggests is not to look at binary search just as an algorithm to find an exact match to some item in a list but rather as an search algorithm that gets us the lowest value from a range of values where a particular condition is True. We can define the condition in our own different way based on the problem.

Lets start with a template which I will use in an example to explain what I really mean above. We can now just change a very few things in the below given template namely wthout worrying about the less than and greater than signs: Condition, Range and the return statement.

Here is the template:

def binary_search(array):
    def condition(value):
        pass
    # could be [0, n], [1, n] etc. Depends on problem
    left, right = min(search_space), max(search_space)
    while left < right:
        mid = left + (right - left) // 2
        if condition(mid):
            right = mid
        else:
            left = mid + 1
    return left

So what does the above template do? Given some condition, and a search space, it will give you the minimum value in the search space that satisfies the given condition. This value is the left in this code.

Better explain this with an example: Lets rephrase our problem of finding an element in a sorted array as: Find the position of the first element in the sorted array that is ≥ target.

Here we define 3 things:

1. Condition: array[value] >= target

2. range: Since the indices in arrays can range from 0 to n-1.

3. Return statement: We have gotten the index of the leftmost element that is ≥target. To answer our question we can just use a if-else loop on this index.

def binary_search(array):
    def condition(value):
        return array[value] >= target
    left, right = 0, n-1
    while left < right:
        mid = left + (right - left) // 2
        if condition(mid):
            right = mid
        else:
            left = mid + 1
    if array[left] == target:
        return left
    else:
        return -1

So, in the above we got the minimum index in the sorted array where the condition value ≥ target is satisfied. Graphically:

Binary Search The Answer?

So, now we understand Binary search a little better, let us see how this generalises to problems. And how you can think of Binary search as a solution search.

Koko Eating Bananas

From the problem definition on Leetcode :

Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.
Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return the minimum integer k such that she can eat all the bananas within h hours.
Example 1:
Input: piles = [3,6,7,11], h = 8
Output: 4
Example 2:
Input: piles = [30,11,23,4,20], h = 5
Output: 30
Example 3:
Input: piles = [30,11,23,4,20], h = 6
Output: 23

So, how does our Monkey Koko optimize his eating speed? We need to find the minimum speed with which koko could eat so that some condition is specified. See the pattern?

We could try to think of eating speeds as a non-given sorted array and we can search for the minimum value in this array that specifies our condition.

We need to come up with three parts to solve this problem:

1. Condition: We will create a function that returns True,if for a given eating speed k, Koko would be able to finish all bananas within h hour.

2. Range of answers: The minimum eating speed must be 1. And the maximum could be max(piles) based on the problem.

3. What to return? Should return left as that is the minimum value of speed at which our condition is met.

Here is the code:

class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        # Can Koko finish the piles given this speed k?
        def check(k):
            hours_taken = 0
            for n in piles:
                if n%k==0:
                    hours_taken += n//k
                else:
                    hours_taken += n//k + 1
            if hours_taken>h:
                return False
            return True

        left,right = 1 , max(piles)
        while left<right:
            mid = left+(right-left)//2
            if check(mid):
                right = mid
            else:
                left = mid+1
        return left

And that is it. Here we have “Binary Searched the Answer”. And it is applicable to a wide variety of problems. Other such problems you can look at are:

• First Bad Version - LeetCode
• Split Array Largest Sum
• Find the Smallest Divisor Given a Threshold

Conclusion

In this post, I talked about Binary Search. This is one of the most popular algorithms that is asked in Data Structures interviews, and a good understanding of these might help you land your dream job. And while you can go a fair bit in data science without learning it, you can learn it just for a little bit of fun and maybe to improve your programming skills.

Also take a look at my other posts in the series , if you want to learn about algorithms and Data structures. If you want to read up more on Algorithms, here is an Algorithm Specialization on Coursera by UCSanDiego , which I highly recommend to learn the basics of algorithms.

Thanks for the read. I am going to be writing more beginner-friendly posts in the future too. Follow me up at Medium or Subscribe to my blog .

Also, a small disclaimer — There might be some affiliate links in this post to relevant resources, as sharing knowledge is never a bad idea.