Things to see while buying a Mutual Fund

This is a post which deviates from my pattern fo blogs that I have wrote till now but I found that Finance also uses up a lot of Statistics. So it won’t be a far cry to put this on my blog here. I recently started investing in Mutual funds so thought of rersearching the area before going all in. Here is the result of some of my research.

1. Load/No-Load:

Always Buy No Load Mutual Funds

2. Regular/Direct:

There are many differenct sites from where you can buy Mutual funds. Most of these sites take a commision to let you the investor buy and sell from their platform. To overcome this commision you can buy direct Mutual funds from the fund houses themselves. But that would be difficult as their are a lot of fund houses and mmanaging all of that could be quite painful. But with the advent of MFUtility you can buy direct plans from the same platform.

3. Expense Ratios:

The expense ratio is a measure of what it costs an investment company to operate a mutual fund. To see how expense ratios can affect your investments over time, let’s compare the returns of several hypothetical investments that differ only in expense ratio. The following table depicts the returns on a 10,000 initial investment, assuming an average annualized gain of 10%, with different expense ratios (0.5%, 1%, 1.5%, 2% and 2.5%):

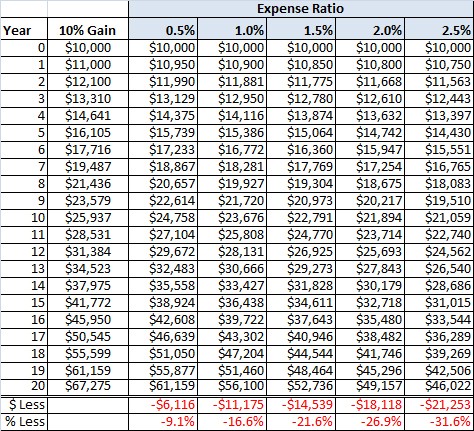
As the table illustrates, even a small difference in expense ratio can cost you a lot of money in the long run. If you had invested 10,000 in the fund with a 2.5% expense ratio, the value of your fund would be 46,022 after 20 years. Had you instead invested your 10,000 in the fund with a lower, 0.5% expense ratio, your investment would be worth $61,159 after two decades, a 0.33% improvement over the more expensive fund. Keep in mind, this hypothetical example examines funds whose only differences are the expense ratios: all other variables, including initial investment and annualized gains, remain constant (for the example, we must assume identical taxation as well). While two funds are not likely to have the exact same performance over a 20-year period, the table illustrates the effects that small changes in expense ratio can have on your long-term returns.

4. Avoid Mutual Funds With High Turnover Ratios:

Mutual fund turnover is calculated as the value of all transactions (buying, selling) divided by two, then divided by a fund’s total holdings. In simpler terms, mutual fund turnover typically measures the replacement of holdings in a mutual fund, and is commonly presented to investors as a percentage over a one year period. If a fund has 100% turnover, the fund replaces all of its holdings over a 12-month period and that bears cost to the investment company in terms of brokerage etc.

5. Look for Ample Diversification of Assets:

Simply owning four different mutual funds specializing in the financial sector (shares of banks, insurance companies, etc.) is not diversification. Don’t own funds that make heavy sector or industry bets. If you choose to despite this warning, make sure that you don’t have a huge portion of your funds invested in them. If it’s a bond fund, you typically want to avoid bets on the direction of interest rates as this is rank speculation.

6. Not Same Fund Family:

Don’t keep all of your funds within the same fund family. Witness the mutual fund scandal of a few years ago where portfolio management at many firms allowed big traders to market time the funds, essentially stealing money from smaller investors. By spreading your assets out at different companies, you can mitigate the risk of internal turmoil, ethics breaches, and other localized problems.

7. Keep Track of various Risk Ratios:

a. Standard deviation:

Standard deviation (SD) measures the volatility the fund’s returns in relation to its average. It tells you how much the fund’s return can deviate from the historical mean return of the scheme. If a fund has a 12% average rate of return and a standard deviation of 4%, its return will range from 8-16%

Computation:

Standard Deviation (SD) = Square root of Variance (V)

Variance = (Sum of squared difference between each monthly return and its mean / number of monthly return data – 1)

b. R-Squared:

R-Squared measures the relationship between a portfolio and its benchmark. It can be thought of as a percentage from 1 to 100. R-squared is not a measure of the performance of a portfolio. A great portfolio can have a very low R-squared. It is simply a measure of the correlation of the portfolio’s returns to the benchmark’s returns.

Computation:

R-Squared = Square of Correlation

Correlation(xy)= Covariance between index and portfolio/(Standard deviation of portfolio * standard deviation of index)

Significance:

• If you want a portfolio that moves like the benchmark, you’d want a portfolio with a high Rsquared.

• If you want a portfolio that doesn’t move at all like the benchmark, you’d want a low R-squared.

General Range for R-Squared:

• 70-100% = good correlation between the portfolio’s returns and the benchmark’s returns

• 40-70% = average correlation between the portfolio’s returns and the benchmark’s returns

• 1-40% = low correlation between the portfolio’s returns and the benchmark’s returns

• Index funds will have an R-squared very close to 100.

• R-squared can be used to ascertain the significance of a particular beta or alpha. Generally, a higher R-squared will indicate a more useful beta figure. If the R-squared is lower, then the beta is less relevant to the fund’s performance

• Values range from 1 (returns are explained 100% by the market) to 0 (returns bear no association with the market)

c. Beta:

A beta of 1.0 indicates that the investment’s price will move in lock-step with the market.

A beta of less than 1.0 indicates that the investment will be less volatile than the market, and, correspondingly, a beta of more than 1.0 indicates that the investment’s price will be more volatile than the market.

For example, if a fund portfolio’s beta is 1.2, it’s theoretically 20% more volatile than the market. Conservative investors looking to preserve capital should focus on securities and fund portfolios with low betas, whereas those investors willing to take on more risk in search of higher returns should look for high beta investments.

Computation:

Beta = (Standard Deviation of Fund x R-Square) / Standard Deviation of Benchmark

If a fund has a beta of 1.5, it means that for every 10% upside or downside, the fund’s NAV would be 15% in the respective direction.

d. Jensens Alpha:

Alpha is a measure of an investment’s performance on a risk-adjusted basis.

Simply stated, alpha is often considered to represent the value that a portfolio manager adds or subtracts from a fund portfolio’s return.

A positive alpha of 1.0 means the fund has outperformed its benchmark index by 1%. Correspondingly, a similar negative alpha would indicate an underperformance of 1%.

Computation:

Alpha = {(Fund return-Risk free return) – (Funds beta) *(Benchmark return- risk free return)}

For example, assume a mutual fund realized a return of 15% last year. The appropriate market index for this fund returned 12%. The beta of the fund versus that same index is 1.2 and the risk-free rate is 3%. The fund’s alpha is calculated as:

Alpha = {(15 -3) – (1.2) *(12- 3)} = 12 - 9 x 1.2 = 12-10.8 = 1.2

Given a beta of 1.2, the mutual fund is expected to be riskier than the index, and thus earn more. A positive alpha in this example shows that the mutual fund manager earned more than enough return to be compensated for the risk he took over the course of the year. If the mutual fund only returned 13%, the calculated alpha would be -0.8. With a negative alpha, the mutual fund manager would not have earned enough return given the amount of risk he was taking.

e. Sharpe Ratio:

Sharpe Ratio measures how well the fund has performed vis-a vis the risk taken by it. It is the excess return over risk-free return (usually return from treasury bills or government securities) divided by the standard deviation. The higher the Sharpe Ratio, the better the fund has performed in proportion to the risk taken by it. The Sharpe ratio is also known as Reward-to-Variability ratio and it is named after William Forsyth Sharpe.

Computation:

SR = (Total Return – Risk Free Rate) / SD Of Fund

For example: Your investor gets 7 per cent return on her investment in a scheme with a standard deviation/volatility of 0.5. We assume risk free rate is 5 per cent. Sharpe Ratio is 7-5/0.5 = 4 in this case

8. And Finally Always Dollar-Cost Average:

Dollar cost averaging is a technique designed to reduce market risk through the systematic purchase of securities at predetermined intervals and set amounts.Instead of investing assets in a lump sum, the investor works his way into a position by slowly buying smaller amounts over a longer period of time. This spreads the cost basis out over several years, providing insulation against changes in market price.

Every investor investment strategy differs. These are just some common guidelines to work your way through the market and making informed decisions while buying Mutual Funds. Normally I work through points 1-6 and get my list to a few mutual funds after which I generally use risk ratios to determine which of the funds I selected might be a winner. I have a bias towards long term investing when it comes to investing so whatever I wrote here must be taken with a grain of salt just as everything related to investment must be. Some of you who are doing this for a longer time than I can also tell me about the various other things I can do. I will try to include those ideas in this post as well.

To Learn more about Mutual funds and investing in general, take a look at the following two gems:

The Editorial review of The intelligent Investor says “Among the library of investment books promising no-fail strategies for riches, Benjamin Graham’s classic, The Intelligent Investor, offers no guarantees or gimmicks but overflows with the wisdom at the core of all good portfolio management” and it rings true in every sense. A must read for everyone looking to invest seriously.

Common Sense on Mutual Funds focusses on Mutual funds exclusively. Lets you understand that investing is not difficult. For the not so involved reader.

Till than Ciao!!!

References:

1. https://www.thebalance.com/picking-winning-mutual-funds-357957
2. http://www.miraeassetmf.co.in/uploads/TermofWeek/Sharpe_Ratio.pdf
3. http://www.miraeassetmf.co.in/uploads/TermofWeek/Beta_SD_RSquared.pdf
4. http://www.investopedia.com